Logical clocks - Lamport Clocks and Vector Clocks

Why do we need logical clocks?

The concept of time is fundamental to our way of thinking about ordering of events in a system. Since physical clocks in a distributed system can drift among each other, it will be very difficult to enforce total ordering among all events in a distributed system across a set of processes.

So logical clocks are introduced to enforce ordering of causal and concurrent (if event is not causal, then it's concurrent) events in distributed systems. Distributed system has set of processes and each process execution is modeled as sequence of events. Processes communicate with each other via messages.

What is causal event?

Causal event is certain event caused due to certain event and hence follows happens-before relationship.

1. if a,b are events in same process and a happened before b, then a<b
2. if a denotes sending of message from process-a and b denotes receiving of that message on process-b, then a<b
3. transitive relationship, if a<b and b<c, then a<c

Lamport Clocks

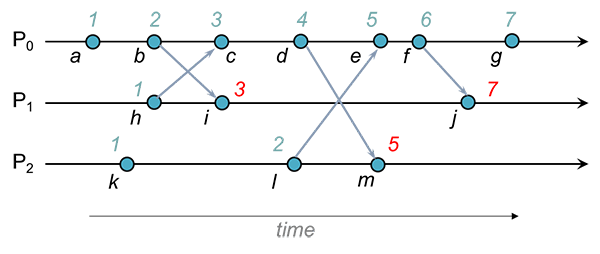
What is Lamport Clocks?

Lamport clocks enforce the happens-before relationship using below rules.

1. It allows assigning sequence numbers, a counter value incrementing from 1, to every event that happens in a single process. Counter is increased before every event.
2. when sending a message from process-a, send the counter value for the event from process-a (lets call it c(a))
3. upon receiving a message on process-b, if c(a)>=c(b), then c(b) = Max(c(a)+1, c(b))

Limitations of Lamport Clocks

1. Multiple events on different processes may have same sequence number
2. We can't determine, just by looking at sequence numbers, if there is causal relationship between 2 events. If a has sequence number 5 and b has 6 doesn't mean a happened before b or b happened as cause of a

Vector clocks

What is Vector Clocks and how is it different than Lamport Clocks?

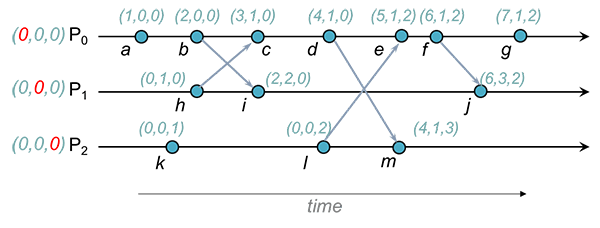
Instead of assigning a simple sequence number, each event is assigned a vector of numbers each assigned to the individual process.

Let's assume (we will get rid of this assumption later) we know number of processes in our system (let's take this number as 3), then the vector value will be (P0,P1,P2).

Sequence of events on P0 will be (1,0,0) (2,0,0) (3,0,0) (4,0,0)

Sequence of events on P2 will be (0,0,1) (0,0,2) (0,0,3) (0,0,4) and so on.

Rules for updating vector clocks for events

1. Before assigning timestamp to event, process increments the counter of its local vector that corresponds to its position in vector. e.g. P2 will increment index 2 in the vector
2. When a process receives an events, it follows rule 1 for its local vector. And then assigns the local vector value by comparing local vector and received vector doing element-by-element comparison. e.g. compare events f and j in schematic below

How can we determine causal relationship just by looking at vector?

1. a->b and a<b, when complete vector for both is not equal and each element of vector a is less than or equal to respective element of vector b e.g. (2,4,6,8) < (3,4,7,9)
2. two events are concurrent and not causal when each element in both vectors is neither less than or greater than other by doing element-by-element comparison e.g. (2,4,6,8) and (1,5,4,9) -> 2>1 but 44, 8<9

What if we don't know number of processes?

Recall that we had to assume that we knew the number of processes in the group so that we could create a vector of the proper size. This is not always the case in real implementations. Moreover, all processes may not be involved in communication, resulting in an unnecessarily large vector.

We can replace the vector with a set of tuples, each of which represents a process ID and its counter:

( { P0, 6 }, { P1, 3 }, { P2, 2 } )